b本篇为方便博主笨比时及时进行算法知识点的一个一个快速回顾

赛前提醒

能用long long和double就用
像什么从0看什么从1看这样的状态设置,怎么方便就怎么来(不一定就要统一,但若要输出记得还原),但一定一定要在开做前就区分好了,再去实现,不然后面会容易混淆的.不过,这些初步设置成啥样也只是实现难度的问题,并不会影响最终结果的话,就切忌一直在这方面思考优化了,既没啥大用还有可能导致自己一直左右手互博而一直浪费不必要的时间,题目进展却一点没有(
真不要吝啬于多处理几个边界情况,要求稳,不用追求一个写法处理好全局情况(也可能本来就不能仅一个写法)
稳定心态,减少失误,能得就得,至少能把自己能力范围内的分100%拿到
先通看一遍,有个整体把握.
三思而后行(思考对了才好实现),一定要花足够多的时间去读题和构思(花多点时间读题思考肯定比在一个错误的思路上进行要好的多!多一分钟好的思考也许能减少五分钟的码量)
- 仔细读题,确保每个字眼都读到读懂
  - 数据范围及分布
  - 极端/边界情况
- 构思代码
  - 多用稿纸辅助思考,推算思路
  - 不要尝试用不熟练的算法,就靠已学尽力做就好
- 实现代码
  - 一遍实现一遍思考极端,边界等情况(极端小数据 ,边界数据等)思路是否仍正确
- 检查
  - 低级错误(变量名,数组清空,初始化赋值,符号,数据类型)
  - 提交前多多测试几个数据,自己捏也好,generate一些也好
  如果怎么找思路上和实现上的错误都找不出来,那么一定是很细微的铸币低级错误,就再重新确认一遍题目要求(最好是一开始就能确定好,如果做题的根基都错了就烷基八蛋了,但碰上这种情况也再去看一遍(你也不知道你第一遍认为的是不是真的就跟题意切合,再揣摩好)),挑着低级错误细细去看,并且把看过的部分就收起来,不要再重复看了!!!那是无意义的浪费时间(除非自己检查的标准有了新变动,那就应该用新标准再去看一遍)
- 有时间的话,对于没有把握的题,不要吝啬去蒙去猜结论,肯定是稳赚不赔的
  - 先暴力搜索+分段(先处理小的,对大的单独优化),再优化(剪枝,记忆化)
  - 加上贪心
  - 打表
  - 找规律
除非还能有把握,不然最后10分钟就全面检查(中间就注意保存),看看好还能不能救(命名,数组大小等)

小知识点

传入常数时注意使用lld强转
一秒认定为2e8
堆上256MB最多可开5e7个int最好不超1e7(所以开大数组时再慎用lld)
erase会返回所删除元素的下一个元素的迭代器,赋值即可
对于递推式,一般而言若由子状态递推,要根据子状态所处位置选择正确的循环顺序.

小技巧

在main()里面用solve()函数,方便运行至中间就结束
学会多去使用空间记录来简化代码量**(本来也就用不完)**
对于二维的状态压缩,可以先用一维的去存储(将二维拆分为一维),在处理时再转化为二维的
若有多次求取而有可能出现重复,则使用记忆化数组记下第一次求的值
根据题目情况,确定好什么从0看什么从1看,最好统一来看更方便,但一定要明确好什么变量怎么看,才方便做题
把bitset当作二进制数串来看即可

铸币小错

实数!=整数!!!要用lf!!!

基础算法

贪心

只看目前何种选择最好就去选(局部的,对于全局来说不一定选择这个就最好,可能现在差点会对全局更好)

证明其正确性即证明局部最优解就是全局最优解(局部最好就对全局最好,一般要独立的或能共同好的)

差分(不同于用树状数组,维护的是变化数组,并非差分)

当需要**多次修改区间O(1)但仅少量查询O(n)**时可用

二维前缀和

注意维护好边界情况,看好是否要减去或是加上(写成区块去看)

向右下加和,块+块-重叠+单点

求取 块-(块+块-重叠)+(边界)

二维差分

差分<->原数组<->前缀和三者之间都可运算互化

二维差分定义式 b[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1]

修改时注意b[x2+1][y2+1]处也要+1

二进制枚举

表示用一个二进制数(虽然短,但其实能对应很多种情况,所以也是独特的)来表示一个子集(相对于总体集合,每个元素选与不选),从而共可能有2的n次方种情况

即为状态压缩,用一个二进制数特别地表示出一个状态

单调队列

元素入队前把队首会破坏区间性和队尾会破坏单调性的元素去掉(队列保存下标即可,调用原数组读取值,否则要用pair)

单调栈

每个元素最多出入一次

元素入栈前把栈顶会破坏单调性的元素去掉

数论

gcd*lcm=a*b

组合数思想

互补性质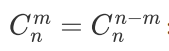 189b3a44f8bcf6b0e687730f596d413d

杨辉三角

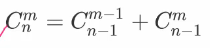
7e32652740f3f8403d4fea252c15d9ed

可用于线性递推二项式系数(先乘后除)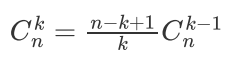 69c41febe0e1fd9d41106447ed434f31

直观解释

2536917b2042b0806ac454700cb38442

Cmn的写法

lld C(lld m,lld n)
{
    if(n==m||m==0) ret 1;//边界情况
    ret (C(m-1,n-1)+C(m,n-1));    
}

字符串

求回文串(接近线性)

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <cmath>
using namespace std;

#define ull unsigned long long
const int N = 2000010, P = 131;

char s[N];
ull h1[N], h2[N], p[N];

ull get(ull h[], ull l, ull r)
{
    return h[r] - h[l - 1] * p[r - l + 1];
}

int main()
{
    int cnt = 0;
    while (scanf("%s", s + 1) && strcmp(s + 1, "END"))
    {
        int n = strlen(s + 1) * 2;
        for (int i = n; i; i -= 2)
        {
            s[i] = s[i / 2];
            s[i - 1] = 'z' + 1;
        }
        s[ ++ n] = 'z' + 1;
        p[0] = 1;
        for (int i = 1, j = n; i <= n; i ++ , j -- )
        {
            h1[i] = h1[i - 1] * P + s[i] - 'a' + 1;
            h2[i] = h2[i - 1] * P + s[j] - 'a' + 1;
            p[i] = p[i - 1] * P;
        }
        ull ans = 1;
        for (int i = 1; i <= n; i ++ )
        {
            ull r = min(i - 1, n - i);
            if (ans >= r || get(h1, i - ans, i - 1) != get(h2, n - (i + ans) + 1, n - i)) continue;
            while (ans <= r && get(h1, i - ans, i - 1) == get(h2, n - (i + ans) + 1, n - i)) ans ++ ;
            ans -- ;
        }
        printf("Case %d: %d\n", ++ cnt, ans);
    }
    return 0;
}

数据结构

树状数组

若用于二维就多套一层循环即可

dp

阶段:从起始阶段转移到目标阶段的若干个子问题序列,每个是解决某个子问题以进行状态转移的解题过程,在一系列的阶段中逐步推进(每个阶段都依赖于前面阶段的结果,需要满足避免重复计算,无后效性)

状态表示f[i][j]:子问题的特征

决策:状态转移方程,可以多根据状态转移的限制来思考出状态转移方程

状态设置要求

只有dp的初始状态按要求设置好了,才能够确保是由初始状态递推而来的答案.

要设置成互无影响的,不重不漏的状态,能划分而确定好局部与全局的关系(部分好能推得全局好,否则换一种状态表示).要确保当使用子问题结果递推时子问题已经完全解决(或者不完全解决也不影响结果,是互相独立的,可以叠加)才可用于递推更新状态

此后,别以为可能会互相囊括冲突,其实因为有维度i,j的限制,每个值都是要看作两两独立的(只是讲求取时不会互相有囊括冲突影响)

满足三个条件：最优子结构，无后效性和子问题重叠。

最优子结构

具有最优子结构也可能是适合用贪心的方法求解。

注意要确保我们考察了最优解中用到的所有子问题。

证明问题最优解的第一个组成部分是做出一个选择；
对于一个给定问题，在其可能的第一步选择中，假定你已经知道哪种选择才会得到最优解(假设要是求得的就会是最优(但其实现在还没求得),那么也一定是由求得的子问题的最优解得到的(即肯定会是由最优继承,不可能有漏解或非最优继承影响)),现在并不用关心这种选择具体是如何得到的.
给定可获得的最优解的选择后，确定这次选择会产生哪些子问题，以及如何最好地刻画子问题空间；
证明在这一种决策下,作为构成原问题最优解的组成部分，每个子问题的解就是它本身的最优解。方法是反证法，考虑加入某个子问题的解不是其自身的最优解，那么就可以从原问题的解中用该子问题的最优解替换掉当前的非最优解，从而得到原问题的一个更优的解，从而与原问题最优解的假设矛盾。

要保持子问题空间尽量简单，只在必要时扩展。

最优子结构的不同体现在两个方面：

原问题的最优解中涉及多少个子问题；
确定最优解使用哪些子问题时，需要考察多少种选择。

子问题图中每个定点对应一个子问题，而需要考察的选择对应关联至子问题顶点的边。

无后效性

已经求解的子问题，不会再受到后续决策的影响。

子问题重叠

如果有大量的重叠子问题，可以记忆化避免重复求解(在当前阶段解决该阶段的总体的子问题需要解决若干个子问题的子问题,而部分子问题的子问题在之前的阶段已经求过了)相同的子问题，从而提升效率(方便由先前状态得出的最优值,判断性继承)。

图论

如果需要将边按边权排序,需要多次建图（如建一遍原图，建一遍反图）可以将边直接存下来，需要重新建图时利用直接存下的边来建图,就用vector e

邻接矩阵只适用于没有重边（或重边可以忽略,如求最短路,就只要看最小的那条边就足够）的情况。(或者能够特殊处理)

其最显著的优点是可以 O(1) 查询一条边是否存在。一般只会在稠密图上使用

邻接表vector e[N],存各种图都很适合除非有特殊需求（如需要快速查询一条边是否存在，且点数较少，可以使用邻接矩阵）。

链式前向星,不能快速查询一条边是否存在，也不能方便地对一个点的出边进行排序。优点是边是带编号的.而且如果 cnt 的初始值为奇数，存双向边时 i ^ 1 即是 i 的反边(且一定这么关联)（常用于网络流）